|
| நீக்கமற நிறையா நெருக்கங்கள் |
   |
- வாஞ்சிநாதன்![]() | |![]() பிப்ரவரி 2005 பிப்ரவரி 2005![]() | |![]() |
|
|
|
|
பள்ளிக்கூடத்தில் படிக்கும் உங்க ளுடையை நான்கு வயதுக் குழந்தை எத்தனை முறை பென்சிலைத் தொலைத்திருக்கிறான்? நேற்று நீங்கள் சென்று வந்த கல்யாண விருந்தில் எத்தனை பேர் இரண்டாவது முறை பாயசம் வேண்டுமென்று கேட்டு வாங்கிச்சாப் பிட்டார்கள்? கடந்த 70 ஆண்டுகளில் அமெரிக்கா எத்தனை நாடுகளின் மீது படையெடுத்து குண்டு வீசியுள்ளது?
இதுபோன்ற கேள்விகளுக்குப் பதிலளிப் பது கடினமென்றாலும், பதிலாகக் கூறப்படும் எண்களெல்லாம் எண்ணிக்கையைத் தெரிவிக்கும் முழு எண்கள் (positive integers or whole numbers) எனப்படுகின்றன. பதினொன்று, முந்நூற்றியேழு, நாற்பது இவையெல்லாம் இவ்வகையிலடங்கும்.
இப்போது வேறுவிதமான கேள்விகள். கிளியோபாட்ராவின் மூக்கின் நீளமென்ன (சென்டிமீட்டரில்)? சென்ற ஆண்டு மொத்தத்தில் எவ்வளவு காபி குடித்தீர்கள் (லிட்டர்களில்)? தோராயமாக இல்லாமல் துல்லியமான விடையளிக்க வேண்டு மென்றால் முழு எண்கள் ஒத்து வராது. இதற்கு அளக்கும் எண்கள் வேண்டும். இவற்றை ஆங்கிலத்தில் real numbers என்பதால் மெய்யெண்கள் என்று நாம் வழங்குகிறோம். இவ்வகையில் 5.8337, 146.751 என்ற எண்களைக் கூறலாம். பெரும்பாலும் தசம எண்களாக (decimal numbers) இவற்றை எழுதுவது வழக்கம்.
மெய்யெண்கள் தசம வடிவின்றி பின்ன வடிவத்திலும் (fractions) சிலசமயம் எழுதப் படும். உதாரணமாக 1/4, 67/50, 365/7. இவற்றில் முதலிரண்டை 0.25, 1.34 என்று எழுதலாம். மூன்றாவது எண்ணை தசம எண்ணாக எழுத முற்படும்போது தசம இலக்கங்கள் முடிவின்றி வந்து கொண்டேயிருக்கும்:
ஒரு வருடத்தில் எத்தனை வாரங்கள் என்பதற்கான விடை முழு எண்ணாக இல்லை. இந்த பின்ன எண்ணை தசமமாக்க முயல்கையில்
365/7 = 52.142857142857142857142857...
என்று 142857 என்ற ஆறிலக்கங்கள் நிற்காமல் மீண்டும் மீண்டும் தொடர்ந்து வந்து கொண்டேயிருக்கின்றன.
ஏன் 1/3 என்ற எளிய பின்னமே, கைக்கு அடக்கமான தசம எண்ணாக இருக்க மாட்டேனென்று பிடிவாதம் பிடிக்கிறது:
1/3 = 0.333333........
இந்தக் கட்டுரையின் நோக்கம் எண்களில் இன்னும் சில நுட்பமான வகைகள் உள்ளன என்பதைக் காட்டுவதுதான்.

ஆரம்பப் புள்ளியாகத் தரையில் ஏதேனும் ஒரு புள்ளியை வைத்துக்கொண்டு அதிலி ருந்து கிடையாக நேர்கோட்டை வரைந்து கொள்ளவும். (வரையறையின்றி நீண்டு கொண்டே செல்வதாகக் கொள்வோம்)
இதை மெய்யெண்கோடு என்கிறார்கள் (உண்மையில் இருபுறமும் நீட்ட வேண்டும், ஆனால் நமக்கு ஒருபுறம் நீண்ட கோடே போதுமானது). இப்போது அந்த கோட்டி லிருக்கும் எந்தப் புள்ளியின் தூரத்தையும் ஆரம்பப் புள்ளியிலிருந்து அளந்து மீட்டரில் விடையைக் கூற முற்பட்டால் தசம எண்கள் தான் கிடைக்கும்.
இப்படி வரும் எண்ணின் இலக்கங்கள் முடிவுற வேண்டுமென்றோ, அல்லது முடிவுறாமல் சில இலக்கங்களே மீண்டும் மீண்டும் வருமென்றோ (cyclic patterns) எதிர்பார்க்க முடியாது. அதாவது சில மெய்யெண்களை பின்ன எண்களாக (முழு எண்களின் விகிதமாக - ratio of whole numbers) எழுத முடியாது. அவற்றை விகிதமுறா எண்கள் (irrational numbers) என்கிறார்கள். இதன் ஆங்கிலப் பெயரைக் கேட்டு பகுத்தறிவில்லாதது என்று நினைக்க வேண்டாம்! ratio அல்லாதது என்ற பொருளில் கூறப்பட்டுள்ளது, அவ்வளவு தான்.
இப்போது 2 என்ற எண் விகிதமுறா எண் என்பதை நாம் சோதித்துப் பார்த்து விடுவோம். இது பின்ன எண்ணாக இருக்குமேயானால், a/b என்று முழு எண்களின் விகிதமாக எழுதமுடிந்திருக்கும். இதில் a,b இரண்டையும் வகுக்கும் எண்கள் இருந்தால் அவற்றை நீக்கி விடலாம்: அதாவது 70/105 என்ற எண்ணில் 5 நீக்கி 14/21 என்று சுருக்கலாம். மீண்டும் இதில் 7ஐ நீக்கி 2/3 என்று சுருக்கலாம். இதன்படி எந்த பின்ன எண்ணையும் இப்படிப்பட்ட நீக்கங்களையெல்லாம் முடித்த பின் சுருங்கா பின்னமாக (irreducible fraction) எழுத முடியும்:
எனவே a/b என்ற அந்த இரண்டின் வர்க்க மூலத்தைச் சுருங்கா வடிவமானதாக எடுத்துக் கொள்வோம். இதில் இரண்டுமே இரட்டைப்படை எண்ணாக இருக்க முடியாது. இருந்தால் அவ்விரண்டையும் 2ஆல் வகுத்துச் சுருக்க முடிந்திருக்கும். ஏதாவது ஒன்று ஒற்றைப்படையாக (odd number) அல்லது இரண்டுமே ஒற்றைப் படையாக இருக்க வேண்டும்.
a/b = 2
அதாவது a/b என்பதன் வர்க்கம் 2 என்ற எண்.
a2/b2 = 2
a2 = 2b2
இப்போது வலப்புறம் 2ஆல் பெருக்கப்பட்ட எண் இருப்பதால் இடப்புறமுள்ள எண் இரட்டைப்படையாக இருக்க வேண்டும்.
ஒற்றைப்படை எண்ணாக a இருந்தால் இடப்புறமுள்ள a2உம் ஒற்றைப்படையாக இருக்க வேண்டியிருக்கும். எனவே a இரட்டைப்படையாக இருக்க வேண்டும். இதன் காரணமாக a2 என்ற எண் 4இன் மடங்காக இருக்க வேண்டும். அதாவது a = 2c, என்று இரட்டைப் படை யெண்ணாக இருந்தால் a2 = 4c2 என்றாகிறது. |
|
|
எனவே 4c2=2b2 என்பதில் 2ஐ நீக்கி 2c2=b2 என்று பெறலாம். இப்போது முன்பு வாதிட்டபடியே b என்ற எண் ஒற்றைப் படையாக இருக்க முடியாது (இருந்தால் b2 என்ற ஒற்றைப் படையெண் எவ்விதம் 2c2 இரட்டைப் படியெண்ணுக்குச் சமமாக இருக்க முடியும்?) எனவே bயும் இரட்டைப் படை எண்தான். இப்போது a/b என்ற சுருங்காப் பின்னத் திலிருந்து தொடங்கியும் a,b இரண்டும் இரட்டைப்படை எண்கள் என்ற பேத்த லான முடிவுக்கு வந்து விட்டோம். இதற்குக் காரணம் a2/b2 = 2 என்ற அடிப்படையில் தொடங்கியதுதான். எனவே வர்க்கம் 2ஆக இருக்கும்படி எந்த சுருங்காப் பின்னமும் இல்லை என்பது நிருபணமாகி விட்டது. அதாவது 2இன் வர்க்கமூலம் விகிதமுறு எண் இல்லை.
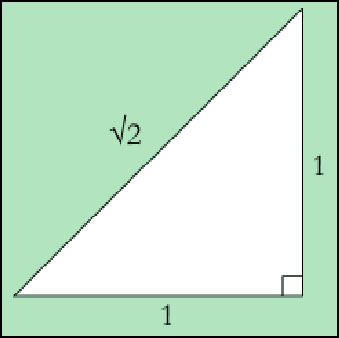
வரைகணிதத்தின் பிதாகரஸ் கூற்றின்படி (Pythogorus theorem) 1செமீ பக்க அளவுள்ள சதுரத்தின் மூலைவிட்டம் (diagonal) 2 செமீ இருக்க வேண்டும்.
எனவே 2 என்ற தூரத்திலுள்ள புள்ளியை அளந்து குறிக்க இயலும். இதைக் கணக்கிட முயன்று 1.41421356..... என்று பார்த்தால் சுழன்று வராமல் எங்கெங்கோ இலக்கங்கள் சென்று கொண்டேயிருக்கும். இதில் வேடிக்கை என்னவென்றால் பின்ன எண்கள் மிகவும் நெருக்கமானவை. அதாவது மெய்யெண் கோட்டில் விகிதமுறு எண்கள் மிகவும் அடர்ந்து இருக்கின்றன. இரண்டு பின்ன எண்களைக் கொடுத்தால் அவை யிரண்டிற்குமிடையே மற்றோர் பின்னத் தைக்காண இயலும். இரண்டையும் ஒரே அடியெண்ணின் மூலம் (common denominator) எழுதிய பிறகு மேலும் கீழும் பத்தால் பெருக்கினால் இடையே நிறைய பின்ன எண்களைக் காணலாம்:
1/2 & 1/3
1/2 = 3/6 = 30/60
1/3 = 2/6 = 20/60
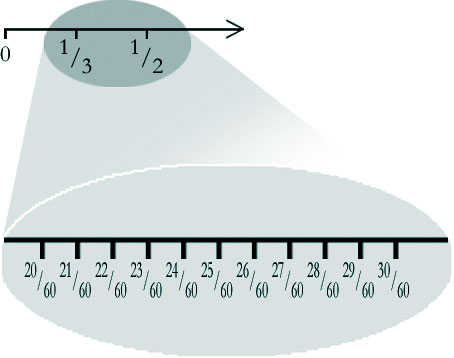
இப்போது 21/60,22/60,....,29/60 என்று பல எண்கள் 1/3க்கும் 1/2க்கும் இடையே உள்ளன. என்னதான் இப்படி விகிதமுறு எண்கள் தன் படைகளை எங்கும் நெருக்கிக் கொண்டு நிற்கச் செய்தாலும் ஆங்காங்கே 2 போன்ற விகிதமுறா எண்கள் இடுக்கைக் கண்டு ஒளிந்து கொண்டு நிற்கின்றன.
Rational numbers are dense and are packed very closely to each other. Yet irrational numbers are squeezed in tiny gaps among them. இதைத்தான் என்னுடைய கணிதப் பேராசிரியர் நகைச்சுவையாக மனிதன் எவ்வளவுதான் பகுத்தறிவுள்ளவனாக இருந்தாலும் அவனிடையே பகுத்தறிவுக்கு முரணான அம்சங்கள் ஒளிந்து கொண்டிருக்கின்றன என்பார்!
பின்னங்கள் பன்மடங்காய்ப் பெருகி நெருங்கிடினும் சின்னதோர் இடுக்குண்டாம் தேர்.
வாஞ்சிநாதன் |
|
|
|
|
|
|
|
|
|
|