|
|
|
 டென்னிஸ் பந்துக்கும் டென்னிகாய்ட் விளையாடு பொருளான பிரிமணை போன்ற வளையத்திற்கும் என்ன வேறுபாடு என்பதை எப்படிக் கூறுவது? இதென்ன கம்ப சூத்திரம்? பிரிமணையில் நடுவே ஓட்டை இருக்கிறது. டென்னிஸ் பந்து முழுமையானதாக இருக்கிறது எனலாம். டென்னிஸ் பந்துக்கும் டென்னிகாய்ட் விளையாடு பொருளான பிரிமணை போன்ற வளையத்திற்கும் என்ன வேறுபாடு என்பதை எப்படிக் கூறுவது? இதென்ன கம்ப சூத்திரம்? பிரிமணையில் நடுவே ஓட்டை இருக்கிறது. டென்னிஸ் பந்து முழுமையானதாக இருக்கிறது எனலாம்.
என்னுடைய ஒன்பதாம் வகுப்பு ஆசிரியர் அவர் சஞ்சரித்துக் கொண்டிருக்கும் பண்டை இலக்கிய நூல்வெளியிலிருந்து அபூர்வமாய் இறங்கி வந்து தற்காலக் கதையைச் சொல்வதுண்டு.
அமங்கலமானச் சொற்களைத் தவிர்த்தல் பற்றிப் பேசும் போது மளிகைக்கடைச் செட்டியாரின் இயல்பை அவர் கூறியது. கடையில் உப்பு தீர்ந்துவிட்டபோது வாடிக்கையாளரிடம் "உப்பு இல்லை" என்று அவர் சொல்ல மாட்டாராம். "பருப்பு இருக்கிறது" என்பாராம். அல்லது "சாயங்காலம் வாருங்கள், அப்போது தருகிறேன்" என்பாராம்.
செட்டியாருக்கு "இல்லை" என்ற சொல் பிடிக்காதது போல் கணிதவியலாரும் ஓட்டை இருப்பதைப் பெரிதுபடுத்தாமல் அந்த வடிவத்தை எப்படி விளக்குவது என்று முயன்றார்கள்.
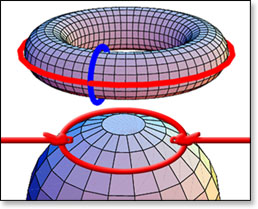
டென்னிஸ் பந்தின் மேற்பரப்பில் வட்டமாய் நூல் இருப்பதாக நினைத்துக் கொள்ளுங்கள். அந்த வட்டம் கொஞ்சம் கொஞ்சமாகச் சிறிதாகிக் கொண்டே வந்தால் ஒரு தருணத்தில் அதன் மையத்தில் ஒரே புள்ளியாகக் குவிந்துவிடும். (சுவாரசியத் திற்காக வட்டத்திற்கு இரு பிடிகளை வைத்து சுருக்கு போட்டு இறுக்குவது போல் படத்தில் காட்டியிருக்கிறோம்).
சிறிதாகும் போது வட்டம் பந்தின் மேற்பரப்பிலேயே மேவியிருக்க வேண்டும் என்பது கட்டுப்பாடு. (படம் 1அ)
இதே சுருக்கு வேலை இந்த பிரிமணையிடம் பலிக்காது. என்னதான் சரித்து, சாய்த்து, அசைத்து, நெளித்து அந்த வட்டத்தைச் சிறிதாக்க முற்பட்டாலும் அதை ஒற்றைப் புள்ளியாய் அமுக்கி வைக்க முடியாது. (படம் 1ஆ)
ஓட்டை வயிற்றுக்காரன் என்று சொல்வதற்குப் பதில் இப்படிச் சொல்வது தன்னிலையில் குன்றாத அதன் புகழை வெளிக் கொணர்ந்துள்ளது பார்த்தீர்களா? இதே குணம் தேநீர்க் கோப்பைக்கும் உண்டு. கோப்பையை வரிந்திருக்கும் வட்டத்தையும் அல்லது அதன் பிடியில் சுற்றியுள்ள வட்டத்தையும் ஒன்றி லிருந்து மற்றதற்கு நகர்த்தி வரலாம். அதாவது ஒரு வளையத்தில் ஒரு பாகம் தடித்து அதைக் குழியாக்கி ஒற்றைப் பிடிக் கோப்பையாக மாறியதாகக் கருதலாம்.
இது என்ன, கண்ணிற்கு முன்னே உள்ளங்கை வடையென தெரிவதற்கு இப்படி ஒரு வரையறை; வீம்புக்குச் செய்வது போல் தோன்றலாம். இந்த பிரிமணைக்குப்
பதிலாக நவகிரகங்களிலொன்றான, (தசகிரகங்களென்று சொல்ல வேண்டுமா?) சனியின் வளையத்தில் நாம் இருப்பதாக கற்பனை செய்து கொள்வோம். பூமி எவ்வாறு நம் வெற்றுக் கண்பார்வைக்குத் தட்டையாகத் தோன்றுகின்றதோ, அது போல் அந்த சனி வளையத்தின் மேல் அமர்ந்து பார்க்கும்போது இந்த ஓட்டை இருப்பதை நாம் உணர மாட்டோ ம். அதாவது ஒரு பொருளின் வடிவத்தை அதைக் கொண்டே விவரிக்க யத்தனிப்பதுதான் இதன் நோக்கம். அந்த பொருளின் வெளிப்புறம் உள்ளது தான் அந்த "ஓட்டை". வெளியே பார்க்காமலே ஒரு பொருளைப் பற்றிக் கூறுவதுதான் சரியான அணுகுமுறை. (நானும் என் மனைவியிடம் நம்மிடம் அடுத்த வீட்டுக்காரன் போல் கார் இல்லை அது இல்லை என்று சொல்லாதே, நமக்கு வீட்டுக்குள்ளே என்னென்ன வெல்லாம் இருக்கிறது பார் என்று சொல்கிறேன்; எங்கே அதைப் புரிந்து கொள்கிறார்கள்). அடுத்தது இரு புறமும் பிடிகள் அமைக்கப்பட்ட கோப்பையைக் காண்போம் இப்போது, வலது புறப் பிடியில் சுற்றியுள்ள வட்டத்தை நகர்த்தி இடப்புறம் மாற்ற முடியாது. அதாவது இந்த வடிவத்தில் வரிந்துள்ள சுருக்குகளில் இரு பிரிவுகள் உள்ளன. (படம் 2) இதைத்தான் நாம் இரு ஓட்டைகளாகக் காண்கிறோம்.
ஒரு வடிவத்தின் பரப்பில் அமைந்த தடத்தை (சுருக்கை) நெறித்து ஒரு புள்ளியில் குவிக்க இணங்கும் வடிவங்களைக் கணிதவியலார் தடங்குவித் தலம் (simply-connected topological space) என்று கூறுகிறார்கள். |
|
|
 நாம் இதுவரை விவாதித்ததெல்லாம் பந்தின் மேற்பரப்பைப் பற்றிதான். அதாவது நாம் டென்னிஸ் பந்தும், சோப்பு நுரைக் குமிழியும் ஒன்றே என்று கருதலாம். அதாவது இரு பரிமாணப் பொருள் பற்றி (அதைத் தட்டையான தளத்தில் அடை தட்டி வைக்க முடியாமற் போனாலும் அது இரு பரிமாணப் பொருள்தான். ஜிம்னாஸ்டிக் விளையாட்டில் மெல்லிய கயிற்றைப் புகை நெளிவதைப் போல் சுழற்றி முப்பரிமாண வெளியில் மேவச் செய்தாலும் அது ஓர் ஒற்றைப் பரிமாணப் பொருள்தான்). எனவே சோப்புக் குமிழி என்பது இரு பரிமாணக் கோளம். இதே போல் மூன்று பரிமாணக் கோளத்தை மனத்தளவில் கற்பனை செய்யலாம். அது "நான்கு பரிமாண வெளியில் ஒரு மையத்திலிருந்து சம தூரத்திலமைந்த புள்ளிகளின் தொகுப்பு." இது நாம் வாழும் பிரபஞ்ச வெளியில் மேவாதது. நாம் இதுவரை விவாதித்ததெல்லாம் பந்தின் மேற்பரப்பைப் பற்றிதான். அதாவது நாம் டென்னிஸ் பந்தும், சோப்பு நுரைக் குமிழியும் ஒன்றே என்று கருதலாம். அதாவது இரு பரிமாணப் பொருள் பற்றி (அதைத் தட்டையான தளத்தில் அடை தட்டி வைக்க முடியாமற் போனாலும் அது இரு பரிமாணப் பொருள்தான். ஜிம்னாஸ்டிக் விளையாட்டில் மெல்லிய கயிற்றைப் புகை நெளிவதைப் போல் சுழற்றி முப்பரிமாண வெளியில் மேவச் செய்தாலும் அது ஓர் ஒற்றைப் பரிமாணப் பொருள்தான்). எனவே சோப்புக் குமிழி என்பது இரு பரிமாணக் கோளம். இதே போல் மூன்று பரிமாணக் கோளத்தை மனத்தளவில் கற்பனை செய்யலாம். அது "நான்கு பரிமாண வெளியில் ஒரு மையத்திலிருந்து சம தூரத்திலமைந்த புள்ளிகளின் தொகுப்பு." இது நாம் வாழும் பிரபஞ்ச வெளியில் மேவாதது.
இரண்டுக்கும் மேற்பட்ட பரிமாணங்களைக் கொண்ட வடிவங்களை ஆய்வதற்குச் சுருக்குகள் மட்டும் போதாது. மூடுபோர்வை கள் (சுருக்கின் இருபரிமாண நண்பன்) என்று ஒரு வரிசையே இருக்கிறது. (Higher homotopy groups) சென்ற நூற்றாண்டின் தொடக்கத்தில் பாங்கரே (Henri Poincarளூ) என்ற பிரெஞ்சு அறிஞர் மூன்று பரிமாண வடிவங்களைப் பற்றி ஒரு கருத்தை வெளியிட்டார். இதே போல் சுருக்குகளை நெறிக்க முடிந்தால் அந்த முப்பரிமாண வடிவம் முப்பரிமாணக் கோளமாகத்தான் இருக்க முடியும் என்று அவர் கூறினார். அவரால் அதை நிரூபிக்க முடியவில்லை.
ஸ்டீபன் ஸ்மேல் என்பவர் ஐந்துக்கு மேற்பட்ட பரிமாணங் கொண்ட வடிவங்களில் சுருக்கு நெறியும் தன்மை, மூடுபோர்வை குவியும் தன்மை,... இவையெல்லாம் இருந்தால் அது அதே பரிமாணக் கோளம் என்பதை நிரூபித்தார். அதன் பலனாக மாஸ்கோவில் 1966இல் நடந்த உலகக் கணிதவியலார் மாநாட்டில் ஃபீல்ட்ஸ் பதக்கத்தையும் பெற்றார். ஆனால் இந்த மூன்று பரிமாண வடிவம்தான் இத்தனை வருடம் இழுத்து விட்டிருக்கிறது.
பெட்டி செய்தி:
"தடங்குவியும் முப்பரிமாண வடிவங்கள் கோளங்கள்" என்ற பாங்கரேயின் (Henri Poincare) கருத்தை நிருப்பித்து நிலை நாட்டிய ரஷ்ய அறிஞர் பெரல்மான், கணித வரலாற்றில் கேள்விப்படாத விதத்தில் நடந்துள்ளார்.
அவர் தன்னுடைய ஆராய்ச்சி முடிவு களை ஆய்வுக்கட்டுரைகளை வெளியிடும் இதழ்களுக்கு அனுப்பவில்லை. தன்னுடைய வலைத்தளத்திலேயே எல்லோரும் படிக்கலாம் என்று வெளியிட்டுள்ளார்.
அவருடைய இந்த சிக்கலைத் தீர்த்த சாதனைக்காக நான்காண்டுகளுக்கொரு முறை நடக்கும் உலகக் கணிதவியலார் மாநாட்டில் இம்முறை ஸ்பெயின் நாட்டில் மாட்ரிட் நகரில் ஆகஸ்டில் நடைபெற்றது அவருக்கு ஃபீல்ட்ஸ் பதக்கம் வழங்க முடிவு செய்தனர். அதை அவர் ஏற்க மறுத்து விட்டார். இப்பரிசை வாங்கிக்கொண்டால் பெரிய சாதனை புரிந்து அதற்கான மிகப் பெரிய பரிசை பெற்று, உலகத்து கணித அறிஞர்களுக்கெல்லாம் செல்லமான வனாகிவிடுவேன். அதில் எனக்கு விருப்பமில்லை. ஓசைப்படாமல் பணி செய்வதும், செய்த பணியால் ஒரு சிக்கலைத் தீர்த்ததிலும் உண்டான மனநிறைவும் எனக்குப் போதும் என்று விட்டார். கணிதவியலாரைப் பற்றியும் அவர்களில் சிலரின் போட்டி மனப்பான்மை, ஏற்றுக் கொள்ள இயலாத ஏமாற்றுத் தனத்தையும் என்னால் பார்த்துக் கொண்டு சும்மா இருக்க முடியாது என்று காரணம் கூறியிருக்கிறார்.
நாற்பது வயதாகும் இவர் 16ஆம் வயதில் சோவியத் நாட்டுக் குழுவில் இடம் பெற்று உலகக் கணித ஒலிம்பிக் போட்டியில் தங்கப் பதக்கத்தை வென்றார். லெனின் கிராடில் (இப்போது செயின்ட் பீட்டர்ஸ்பர்க்) பி. எச்.டி பட்டம் பெற்று சில வருடங்கள் அமெரிக்காவில் பல பல்கலைக் கழகங்களின் அழைப்பை யேற்றுப் பணிபுரிந்து அதன் பிறகு ரஷ்யாவிலேயே தங்கியிருக்கிறார். இனிமேல் அமெரிக்கா வரப் போவ தில்லை என்றிருக்கிறாராம். அங்கே சென்றால் நான் வேலை தருகிறேன் என்று பல பல்கலைக் கழகங்கள் போட்டி போட்டுக் கொண்டு அவருக்குத் "தொல்லை தருகின்றன"வாம். மிகவும் நன்றாக வயலின் வாசிப்பாராம்.
புதிய நூற்றாண்டில் கணிதத்தில் தீராத சிக்கல்களில் கடினமானவை ஏழைத் தேர்ந்தெடுத்து க்ளே கணிதக் கழகம் பரிசை அறிவித்தது. அந்த ஏழில் எதைத் தீர்த்தாலும் ஒரு மில்லியன் டாலர் பரிசென்று அறிவித்திருக்கிறது. அந்த ஏழில் ஒன்றுக்கு விடையைக் கண்டு பிடித்திருந்தும் பெரல்மான் அந்த பரிசைப் பற்றி முனைப்பின்றி இருக்கிறார்.
வாஞ்சிநாதன் |
|
|
|
|
|
|
|
|
|
|