ஏழடி நீளமும் மூன்றடி அகலமும் கொண்ட செவ்வகத்தின் பரப்பளவு 21 சதுர அடி என்றும் சுற்றளவு 20 அடி என்றும் உடனே கூறிவிடுகிறோம். ஆனால் அதன் மூலை விட்டத்தின் நீளமென்ன? பத்துக்குள்ளே நம்பர் ஒன்று சொல்லு என்பது சரி யென்றாலும் எந்த எண்? பள்ளிக்கூடக் கணிதத்தில் படித்த பிதாகரஸ் தேற்றத்தின் படி 72
+32= 49+9 = 58 என்ற எண்ணின் வர்க்கமூலம்தான் அது.
இந்த எண் 7க்கு மேல், ஆனால் எட்டுக் குள் என்பது உடனே தெரிகிறது. ஏழரையா? ஏழரையின் வர்க்கம் =(15/2)2= 225/4, இது ஐம்பத்தாறேகால், 58 இல்லை. 58இன் வர்க்கமூலம் விகிதமுறா எண் (irraational number), பின்ன எண்ணாக எழுத இயலாது.
அதே சமயம் 3 அடி அகலமும் 4 அடி நீளமும் கொண்ட செவ்வகத்தின் மூலை விட்டம்
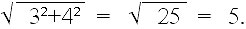
இது முழு எண். இது போல் மேலும் பல சாத்தியங்கள் உள்ளன:
52+122=25+144=169=132;
92+402=81+1600=1681=412;
அதாவது இரண்டு வர்க்கங்களின் கூட்டற்தொகை மீண்டும் வர்க்கமாக அமைவது எவ்வெவ்வெண்களுக்கு என்பது தான் கேள்வி. குறியீடுகளில் இதை x2+y2 = z2 என்ற சமன்பாட்டின் முழு எண் தீர்வுகள் எவை என்று கேட்கலாம்.
அலெக்சாண்டிரியாவைச் சேர்ந்த டய·பான்டஸ் (Diophantus of Alexandria) கி.மு. 300-ம் ஆண்டு வாக்கில் அத்தகைய எண்கள் அனைத்தையும் எப்படி அடைவது என்பதை அவர் எழுதிய நூலொன்றில் விவரித்திருந்தார். அந்நூலின் மொழி பெயர்ப்பை சுமார் இரண்டாயிரம் ஆண்டு களுக்குப் பின் படித்த பிரெஞ்சு நாட்டு வழக்கறிஞர், கணித ஆய்வாளர் பியர் ·பெர்மா வேறு விதமாகச் சிந்திக்க ஆரம்பித்தார்.
x3+y3=z3 என்ற சமன்பாட்டிற்குத் தீர்வுகள் உண்டா, அதாவது இரு கன எண்களின் கூட்டல்தொகை மீண்டும் கன எண்ணாக அமையுமா, அதேபோல் பொதுப்படையாக, இரு n-அடுக்குகளைக் கூட்டி மீண்டும் n-அடுக்கைப் பெற இயலுமா என்று சிந்தித்தார். அதாவது xn+ yn = zn என்ற சமன்பாட்டின் முழு எண் தீர்வுகள் பற்றி.
அவருடைய சிந்தனையில் உதித்ததென்னவோ தெரியவில்லை. அப்புத்தகத்திலேயே ஓரத்தில் "இது சாத்தியமில்லை என்று என்னால் நிரூபிக்க இயலும். அதை விவரித்தெழுத இப் புத்தகத்தின் ஓரத்தில் இடம் போதாது" என்று குறிப்பிட்டார்! அவருக்குப் பின் வந்த ஆய்லர், லக்ரான்ஷ், லஜாண்டர் உட்படப் பலர் 350 ஆண்டுகள் முயன்றும் பலனில்லை. 1995இல் தான் அது முற்றிலுமாக நிரூபிக்கப் பட்டது. ஆனால் அதற்கு மிகவும் சிக்கலான உயர்கணித முறைகள் பல்வேறு விதங்களில் எடுத்தாளப் பட்டுள்ளன.
ஆண்ட்ரூ வைல்ஸ் (Andrew Wiles) என்ற ஆங்கிலேயர் இதைச் சாதித்தார். அவருடைய நீண்ட சிக்கல் மிகுந்த ஆழ்ந்த ஆய்வின் வழி வந்த அத்தீர்வு, நிலவில் மனிதன் காலடி எடுத்து வைத்த சாதனை போல் கணித அறிஞர்களால் போற்றப் படுகிறது.
·பெர்மா படித்த புத்தகத்தில் ஒரு மைல் அகலத்திற்குக் காலியிடம் இருந்தாலும் அத்தகைய நிரூபணத்தை எழுத இட மிருக்காது என்று நகைச்சுவையாகக் குறிப்பிடுவது இப்போது வழக்கமாகிவிட்டது!
எனவே அதை விவரிக்க நாம் முயலாமல், அதன் விளைவுகளில் ஒன்றை மட்டும் குறிப்பிடுவோம். எண்கோட்டில் பின்ன எண்கள் அடர்ந்து இருப்பதை இரு மாதங்களுக்கு முந்தைய கட்டுரையில் பார்த்தோம். அதேபோல் இரு பரிமாணங் களில், அதாவது (x,y) தூரங்களால் குறிப்பிடப்பெறும் சமதளத்தில் (plane or Cartesian plane) இரண்டும் பின்ன எண்களாகக் கொண்ட புள்ளிகள் அடர்ந்து இருக்கும்.
இப்போது இதில் ஓர் ஆச்சர்யத்தைக் காணலாம்.
X3+Y3=Z3 என்ற மூன்று மாறிகள் (variables) கொண்ட சமன்பாட்டின் முழு எண் அல்லாத தீர்வுகளை (real number solutions) எடுத்துக் கொண்டு Z ஆல் அம்மூன்றையும் வகுத்து,
x=X/Z, y=Y/Z, z=Z/Z=1 என்று கொண்டால், x3+y3= 1 என்ற சமன்பாட்டின் தீர்வுகள் கிடைக்கும்.
உதாரணமாக, 23+ 33= 31 என்பதிலிருந்து,
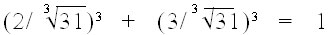
என்பதைப் பெறலாம்.
எனவே, 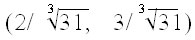 என்ற புள்ளி x3+y3= 1 என்ற வரைபடத்தில் (graph of the curve) அமையும். என்ற புள்ளி x3+y3= 1 என்ற வரைபடத்தில் (graph of the curve) அமையும்.
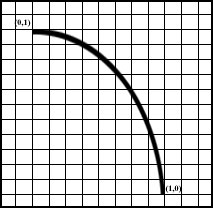
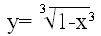 என்பதன் தோராயமான வரைபடம் என்பதன் தோராயமான வரைபடம்
இவற்றையெல்லாம் திரட்டி (0,1) இலிருந்து (1,0) வரை உள்ள படப்பகுதியை நோக்கினால், வரைந்தால், அது அத்தனை நெருக்கமான பின்ன எண் புள்ளிகளை யெல்லாம் ஏய்த்துவிட்டு விகிதமுறா எண்களால் அமைந்த புள்ளிகளின் வழியே இடுக்கில் புகுந்து சென்றுவிடும் என்பது தான் அந்த அதிசயம்.
அதாவது ஒரு மணல் மூட்டையில் ஒரு நூல்கண்டைப் பிரித்து இடுக்கில் இழையோடுவதைப் போலிருக்கும். இந்த "கயிறு விடுதல்" நம் கற்பனையில் எட்டுவதாயிருந்தாலும் செய்வது எவ்வளவு கடினம்.
ஆனால் இந்த வரைபடத்தில் மிகவும் எளிய சமன்பாட்டின் தீர்வுகளே இந்த இடுக்குகளைக் கண்டு புகுந்துவிடுவதுதான் விந்தை!
இதைப்பற்றி மேலும் அறிந்து கொள்ள சுவாரசியமான புத்தகம்.
Fermat's Enigma by Simon Singh
வாஞ்சிநாதன் |